Sound-meaning associations across more than 4000 languages

My friend Damián ‘blasé Damián’ Blasi published a paper in Proceedings of the National Academy of Sciences this week, with Søren Wichmann, Harald Hammarström, Peter Stadler and Morten Christiansen, available here.

The paper was on how there are common sounds that languages across the world tend to use in particular words.  An example is the word ‘nose’, which tends to contain the nasal consonant 'n' more than expected by chance.  The word for 'horn' often has a 'k', reminiscent of the 'bouba/kiki' effect, where people who are asked to use the labels 'bouba' and 'kiki' to describe the two shapes below will tend to use 'kiki' for the jagged shape on the left.

The word for 'small' often has an 'i', as if the lips are being placed together to indicate size in the same way that finger tips can:

The word for 'breast' often has a 'm', the reason for which I will not attempt to speculate on.  People have noticed that words for 'mother' also often have a 'm', although that hypothesis could not be tested here because 'mother' is not in the word list they used.

Stranger associations include 'dog' often having a 's', 'fish' having an 'a', 'star' having a 'z', and 'name' having an 'i'.  The authors also find negative associations, such as 'dog' not tending to use the sound 't'.

Why do these associations occur?  One reason may be that words are often deliberately sound-symbolic.  People are good at tasks such as the bouba/kiki task above, without being able to articulate necessarily what the connection is between shapes and sounds.  Languages can exploit these unconscious connections in forming words, such as English words with fl ('fly', 'flutter', 'fleeting') that have something to do with motion, or gl ('glimmer', 'glitter', 'gleam') to do with light.  Languages can have whole classes of ideophones, words that resemble onomatopoeia ('bang', 'whoosh') but which can be very specific and go beyond sound and describe other senses, such as the Ngbaka Gaya loɓoto-loɓoto 'large animals plodding through mud', Korean 초롱초롱 chorong-chorong 'eyes sparkling', or Siwu nyɛk̃ɛñyɛk̃ɛ̃ 'intensely sweet' (see this review).  

A surprisingly diverse set of meanings can therefore be depicted with sounds, in ways that make a certain intuitive sense.  People can guess the meaning of sound-symbolic terms to some extent, even without knowing the language that they are from.  Other studies have found that people are good at guessing the meaning of words in a foreign language to some extent, for instance which out of the Hungarian words kicsi and nagy means 'big' or 'small', suggesting that even basic, conventionalised vocabulary can retain a sound-symbolic component, conceivably because they are descended from words that were once ideophones.

The intuition that some sounds are more likely to be found in certain words is therefore well-known, but it has not been tested across a large language sample with careful statistical controls before.  The predecessor to this paper was a paper by Wichmann, Holman and Brown (2010) which tested this for the first time, but whose statistical methods are rather strange (including controlling for relatedness by attempting reconstructions of words in proto-languages).  

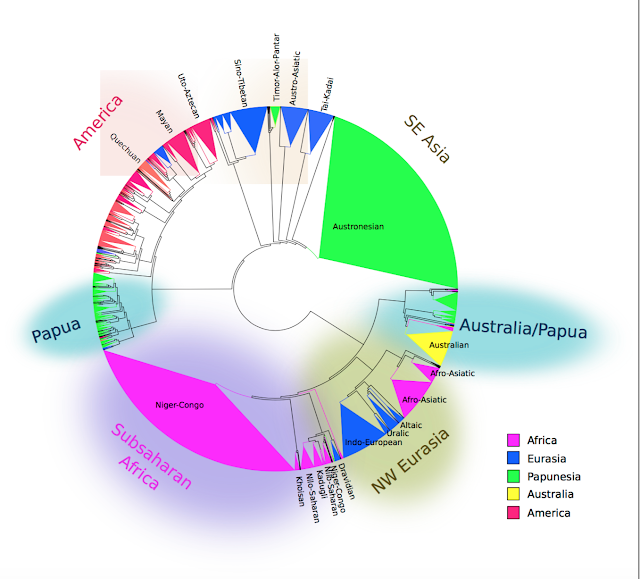
By contrast, the methods of this new paper are very clear and seem sound.  Besides controlling for language families, which I will return to, the authors tested each association in six different areas of the world independently: Africa, Eurasia, Papua New Guinea and the Pacific, and (indigenous languages in) Australia, North America and South America.  They only report associations which are positive in at least three independent areas.

Because they didn't know in advance what sounds would be associated with which meanings, they tested every possible association in the data set.  This is a type of multiple testing, and so you can get some associations by accident (such as the number of drownings in pools correlating with number of films Nicholas Cage appeared in each year).  The authors use a correction for this, which Damián once explained to me in its general form: a data set contains many correlations of varying p-values, some accidentally below 0.05 (i.e. spurious correlations), but many other above 0.05 and going as high as 1.  In a completely random data set, a histogram of the p-values of all correlations looks like this, where the number of 'significant' correlations with a p-value below 0.05 isn't actually any higher than you'd expect for any other interval, suggesting that the p-values below 0.05 are due to chance:

By contrast, in a non-random data-set where 20 variables are correlated with one particular variable, there are many more correlations with p-value below 0.05 than in other intervals, as shown by the spike on the left:

You can test every correlation in the data-set and find out what the expected number of false positives are (i.e. the number of p-values that fall in any particular interval).  You can then choose a threshold such as p<0.0001, below which the number of false positives is going to be small, say 5% of the correlations that you report (as the authors do in this paper).

Finally, they control for word length and the rate that a phoneme is expected to appear in other words of the word list.  They find the frequency that a phoneme is found in a particular word using a genealogically balanced average (i.e. treating each family as one datapoint), and compare it with the frequency that the phoneme appears in other words in the word list.  The ratio of the two is in some cases high, if there is an association of that phoneme with a particular concept, and the significance of that association can be computed by comparing this ratio with the ratio obtained by selecting random words from the same languages.  Word length needs to be controlled for as well, because words differ in how long they are on average ('I', 'me' and 'water' are the shortest words in the list cross-lingustically, and 'star' and 'knee' are the longest).  They correct for this by doing the above test but just comparing words of the same length; and then also performing a test with simulated words of the same length, rejecting any associations between a phoneme and a concept which came out as strongly in the simulated data as in the real data.

I have two minor criticisms of their method of controlling for language relatedness.  An association between a phoneme and a meaning can be inflated by families with a lot of languages such as Indo-European, and the authors deal with this problem by treating each known language family (or isolate) as just one data point, by effectively taking the mean value for that family: for instance, about 82% of the Indo-European languages have 'n' in the word for 'nose' by my count, so Indo-European as a whole gets a value of 0.82.  However, this assumes that Indo-European has a completely flat structure, ignoring the fact that languages belong to sub-groups within Indo-European such as Germanic, Romance and so on.  A single branch of the family with a lot of languages can inflate the value, meaning that they are not controlling for non-independence at lower levels in the family.  

A simple correction for this (one that the authors must have considered but for some reason rejected) is to take average values weighted by branch: for example each node in the family tree gets an average value such as 0.94 in Germanic, 0.82 in Romance and so on, and these are averaged to produce a value at the root, the phylogenetic mean.  This can be estimated using the 'ace' function in the R package 'ape', in which Indo-European gets a much higher value of 0.94.

The second problem is that that slower-changing words are more likely to exhibit sound-meaning correspondences by chance.  Some words change very slowly, such as pronouns and numerals.  In those slow-changing words, there is going to be a higher probability of a particular phoneme being found associated with that meaning, simply because those forms are more similar across languages within a family.  It is still unlikely that many spurious correlations will arise in these words, given that each family is one data point, and the association needs to be in three independent areas; but it may perhaps influence some of the stranger sound-meaning associations that they find, such as 'I' having palatal nasals, or 'one' having 'n' or 't'.  

A possible improvement to their method is to not take mean values, such as how many languages use 'n' in the word for 'nose', but to use family trees to reconstruct whether languages in the past used 'n' in the word for 'nose' and how they changed over time.  As a crude example, here is a plot of a set of Eurasian families (Indo-European, Dravidian, Uralic, Turkic, Mongolic and Tungusic) in a family tree, using the Glottolog classification and then randomly made into a binary tree with branch-lengths each of 1.  Tips with a yellow dot beside them are languages which have 'n' in the word for 'nose'.  You can then use maximum likelihood reconstruction in the R package 'ape' to reconstruct the probability of each ancestral node having 'n' in the word for 'nose', plotted here below by using blue circles whose sizes are proportional to these probabilities.  For example, Proto-Indo-European is reconstructed as having 'n' in 'nose' with a probability of 0.99, in agreement at least with linguists' reconstructions (Mallory and Adams 2006:175).

You can then calculate the rates of gaining and losing 'n' in 'nose' over time.  The rate of gaining 'n' is 0.17, which is higher than for other phonemes such as 0.05 for 't'.  The idea is that 'n' is gained frequently, suggesting that there is something that causes that sound to be associated with that meaning.  By contrast, the association between 'n' and 'one' seems to be more explicable simply by how slow-changing words for 'one' are, as suggested by the plot below.  The rate of gaining 'n' in 'one' is much lower, 0.02, with languages that have it tending to be retaining this association rather than innovating it (again Proto-Indo-European is reconstructed as having it with 0.99 probability).  Similar results for the rates of change are obtained when language families are not assumed to be related but when this is done just within Indo-European.

The authors may have decided not to use phylogenetic methods because of the apparent crudity of the assumptions that you have to make, in the absence of well-resolved binary trees with branch lengths for most families.  But even the crudest solution to that problem, such as my analysis here in R using maximum likelihood with branch lengths of 1 and randomly binarised trees, is a more accurate model than theirs, which effectively assumes entirely flat trees with no internal structure, branch lengths of 1, and no difference between innovation and retention.  The use of phylogenetic methods makes those assumptions more explicit, not more crude.

There are other minor problems, but these are much harder to solve and topics of ongoing research.  For instance, borrowing between languages can create an association between a phoneme and a meaning within a particular macro-area.  The authors explore this possibility by testing how well nearest neighbouring languages predict the presence of particular associations.  Some associations such as using 's' in the word for 'dog' are indeed more likely to occur in a language if they have an unrelated language nearby which also as 's' in the word for 'dog', suggesting that this particular association may have been inflated by borrowing between some language families.  There is finally the possibility that some language families are related to each other, and hence that some form-meaning associations are inherited from ancestral languages.  This has been argued in particular for pronouns, which often use similar sounds across Eurasia in particular.  While it is difficult to correct for this yet without proper cognate-coding between languages in the ASJP (a task I describe here), the authors explore this by comparing the distribution of sound-meaning associations with similarity of word forms overall (as cognates are expected to be more similar than non-cognates).  They also point out that the opposite point holds, that the existence of sound-meaning correspondences casts doubt on some claims about 'ultra-conserved' words.

Despite these possible issues, it is unlikely that many of the correlations they report are spurious, and the results are interesting both in the hypotheses that they confirm (small and 'i', for example), and in the unexpected associations that they discover. There has been plenty of positive coverage of the paper in the media, with particularly good write-ups in The Economist here, The Guardian here, and the Scientific American here.  Science Daily had the witty headline 'A nose by any other name would sound the same', which was also used by the Washington Post and other venues.  The Telegraph and The Sun opted for incoherent clickbait such as 'Humans may speak a universal language, scientists say'. 

While the research does not exactly point to a universal language, it does show that humans are good at perceiving links between form and meaning and use these in language far more than previously thought.  It is not necessarily true that these usages are conscious, and speakers may not be aware that there is anything potentially sound-symbolic about the 'n' in 'nose', for example.  One might speculate that sound-meaning associations are in some cases relics of more consciously sound-symbolic terms such as ideophones.  Another possibility is that words which carry a particular suitable phoneme may be more easily learnt, or somehow preferred in everyday language use, even if this behaviour is unconscious.  Blasi et al.'s paper raises the intriguing question of how associations such as 'n' in 'nose' have come about historically and what it is about speakers' behaviour that favours them.  The other exciting contribution of their paper is a set of sound-meaning correspondences across languages that are as evocative as they are hard to explain - 's' in 'dog', 'z' in 'star', 't' in 'stone', 'l' in 'leaf'.

A further implication of the paper that the authors themselves will perhaps not endorse (or other colleagues of mine who study sound-symbolism such as Dingemanse et al. in this review) is that humans may be good at perceiving links such as between 'k' and jagged shapes because of natural selection for the ability to perceive cross-modal mappings, specifically in the context of acquiring language.  I am not arguing that specific associations such as 'nose' and 'n' are innate, but a general ability to perceive associations across modalities is likely to be innate and have been selected for in the context of acquiring language.  People vary in their ability to guess the meanings of ideophones or words in another language, and there is evidence that this ability is linked with synaesthesia, the condition of having associations across senses such as sounds with colours.  Synaesthesia often runs in families (e.g. this study), giving one example of the way that the ability to make cross-modal mappings with sounds could be subject to genetic variation.  

The fact that competent speakers are good at tasks such as the bouba/kiki task or guessing the meanings of foreign words and ideophones suggests that the genetic variants underpinning these abilities must have become common, perhaps under the influence of selection.  If there was any selection pressure on these abilities in the past, it may have been less on the ability to remember vocabulary (although Imai and Kita (2014) argue that sound-symbolism does help infants learn words) so much as on understanding the concept of spoken communication at all.  Hominids have clearly had some form of communication from 2.5 million years ago which likely used at least manual gesture, as evidenced by tool traditions which require a certain amount of active teaching, leading us to have an enriched ability to understand of the communicative intention of gestures compared with other apes.

The transition to using speech may have similarly created a selection pressure for an instinctive understanding of how sounds can convey meaning.  If so, sound-meaning associations are evidence of shared psychological biases that originally allowed the evolution of spoken language.

External image sources: mouth, gesture, bouba/kiki, Magritte